本贴为非数学专业人士的胡说八道,大家当个乐子一看。
大家会不会觉得乘法交换律很反直觉呢,比如为什么3×8=8×3呢。当然可以用数学归纳法证明乘法交换律(有理数范围内),但是那么做就有点先射箭再画靶子的感觉。那么从直觉上理解乘法交换律可以想象24个小球排成3行8列的方阵,换一个角度看就成了8行3列的方阵。还有一个乘法交换律不那么显然的例子:一支股票先涨5%再跌5%,和同一只股票先跌5%再涨5%,哪种情况赚钱哪种情况亏钱呢,实际上结果都是一样的,因为1.05×0.95=0.95×1.05。
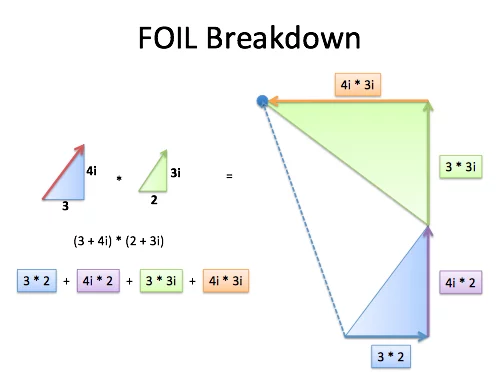
大家高中的时候学到虚数的时候会不会比较懵逼,因为课本上只写了复数的(a+bi)这一种形式,这究竟有什么意义呢?然后在做题或者参考书上才发现复数有三角形式,然后在一通三角函数的推导下发现复数相乘竟然代表了某种旋转!然后呢,实际上还有更直观且本质的理解方式,就是将某数乘i本身就看成一种旋转,那么(1*i*i=-1)就相当于将1按i的方式旋转一次后再按i的方式旋转一次最终达到-1的位置!那么我们就可以根据i=1*i来定义i,也就是说i是1通过某种旋转后到达的位置。我们知道重要的是数集及其运算法则,我们通过扩展实数中的乘法的定义获得了新的带有旋转的乘法,并通过新的乘法与加法将数集从R扩展到了实平面R2上的点。(另外可以证明,R上的任意一个2维向量空间K,如果还是一个结合,交换,具有单位元1且无零因子的环,则必同构于域C。)(详见文章:A Visual, Intuitive Guide to Imaginary Numbers – BetterExplained)
闲话少叙,本帖的目的其实是为了给大家推荐数学科普书的,不是专业的,否则标题就是给大朋友思考的数学问题了。
《数学的雨伞下:理解世界的乐趣》

这本书用通俗的语言介绍了一些比较前沿的数学知识。当然我这么说的话你们大概率是不会去看的,所以我讲一些书里面我觉得比较有意思的东西,然后你们为了看全文就会去看书了。
大家看过很多有四维空间的科幻片,却无论如何也无法在脑中想象出第四个维度,然后就会觉得高维度是个非常神奇的东西。实际上"维"这个字有点被滥用了,物理里面用,物理民科也用,有些讲玄学的也用,数学里面也用,甚至只在数学里的不同语境下的含义也不相同。总而言之,我们现在只考虑简单的空间的维度,也就是零维是无宽度无面积无体积的一个点,一维是指一根无宽度的线,二维是无厚度的一个面,三维是一个体;至于三维以上的空间是长什么样的,可能没有人能够直观地想象出来,只能用某种方式去描述(至少我不知道如何去想象三维以上的空间)。大家可能会觉得每增加一个维度,就是增加一个与之前所有方向都正交的一个方向,比如说从一维到二维是增加了与原有的一条线正交的另一条线。(为什么新方向是正交的呢,因为如果不是正交的方向就可以分解出一个原来的方向而剩下一个与原来方向无关的正交的方向。正交这个角度之所以这么神奇可能因为其对称性。)。那么一维空间里的点可以用一个量来表示,二维空间里的点用两个量来表示,三维空间里的点用三个量来表示,大家是这么认为的对不对?实则不然,我们可以用一根线,来填满整个平面!也就是说,表示一个平面上某个点的位置只需要一个量!是不是感觉一维和二维之间的界限模糊了?我们按照如图所示的方式,无限地将这条线画得更密,于是这条线可以覆盖整个平面。(皮亚诺曲线)
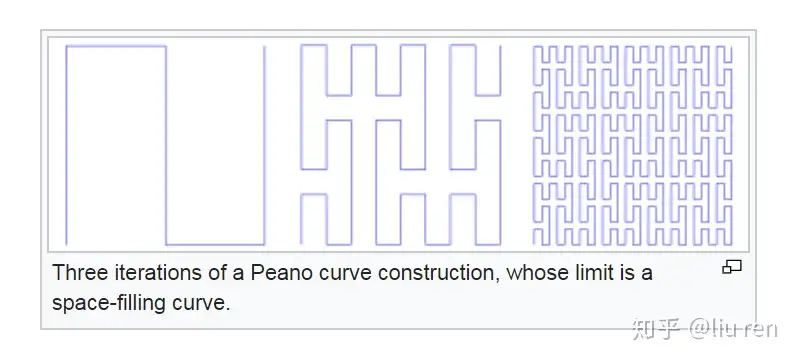
另外我们也可以用非几何的方式证明R与R2是等势的。
《数学故事丛书》张远南
一共有6本,1990年的,可能稍微老了点但还是很有意思的。

我只看了这套书的一小部分,不过给了我很大的视野扩展。我从书里面第一次知道了阿基里斯追龟悖论。
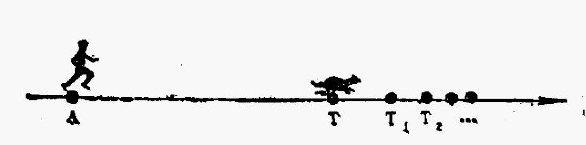
这个故事是这样的:人和龟都向右跑,人跑得比龟快,那么人能不能追上乌龟呢?最开始时人在A点而龟在T点,当人跑到T点时而龟已经爬到了T1点,而当人跑到T1点时龟已经爬到了T2点,如此推理,每次人到达龟之前所在的位置时龟已经又往前爬了一段距离,那么人是永远也追不上乌龟的!按照常识,人跑得比龟快当然能追上乌龟,但是我们上面的思考似乎没有出现问题,究竟是怎么一回事呢?大家自己思考吧!